 , (1)
, (1)
Author: Gábor Kutrovátz
Eötvös University
(ELTE), Budapest
Department of History
and Philosophy of Science
e-mail: wanam@ludens.elte.hu
Poster for the Conference
"Complex Systems in Social and Natural Sciences",
Oct. 15-17, 1999, Kazimierz Dolny, Poland
ABSTRACT
Here I try to build a connection between cosmology and economy from
a thermodynamic point of view.
For this purpose, I introduce the notion of extropy, which is the distance of a physical system from its equilibrium state on the entropic scale.
The extropy of the Universe (the distance from the state of Heat Death) is determined by the interaction of its material components (expanding in their volume), and this extropy determines the rate of thermodynamic processes.
I hope to be able to outline some similarities between cosmological
and economic systems, giving a parallel interpretation of a physical and
an economic problem.
2. Second, I would like to hint some ideas that should illustrate why the analogy between thermodynamics and economics cannot be forced too far, BUT the analogy between cosmology and economics looks more promising.
1.a) The description
of the model universe
We regard the universe
as a system which is determined by three extensive parameters, where these
parameters yield the following expressions:
1. For R:  , (1)
, (1)
where
R is the 'radius'
of the universe (the scale parameter),
G is the gravitational
constant,
r
is the matter
density, and
k
is a constant
that determines whether the universe is open
(k ³
0) or closed (k
< 0);
where
E is the internal
energy of the universe,
p is the pressure
and
V is the volume
(proportional to R3).
We can see here that the internal energy is not constant, because it is transformed into the energy of the gravitational field. I do not say anything in addition to this here, but I shall pursuit this problem in the second part of this poster.
3. We have a third extensive
parameter in the description: it is N, the number of particles
in the universe. Unlike in the case of the other two extensive parameters,
we assume that N is constant.
1.b) The simulation of the model universe
In the universe described in this way, we assume the presence of two matter components:
* atomic hydrogen:
this cools according to R-2,
* (black-body) photon
gas: this cools according to R-1.
(The cooling rates can be derived from physical theories.)
Both components are homogenous
and isotropic, and we suppose that there is an interaction between them:
the strength of this interaction is given by an arbitrary numerical value.
We can now derive a system of differential equations which, assuming that the radius changes according to Eq. 1 above, enables us to derive the following parameters of the system:
R : the radius of
the universe,
Tg
: the temperature of the gas component,
Tr
: the temperature of the radiation component,
S : the total entropy
of the universe.
The system of equations
(see Ch. 1.d) is borrowed from G. Marx and R. Alpher (see
References).
The simulation was done
using the computer program Mathematica.
1.c) The extropy of the model universe
Before we come to the
results of the numerical solution to the system of equations, we introduce
the notion of extropy. Following K. Martinás (see
References), extropy is a state parameter which expresses the distance
of a physical system from its equilibrium state on the entropic scale.
In other words, it measures the entropy production of the fictive process
that takes a physical system to equilibrium with environment. Therefore
it is the difference between the maximal entropy of system and environment
and the total entropy of system and environment:
1.d) The results of the simulation
After the derivation we get the system of equations:
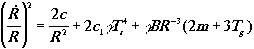 ,
, |
|
 ,
, |
|
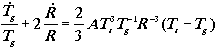 .
. |
|
|
|
|
(B is the barionic number, m is the molecular mass, A is the coefficient of the interaction, Cg and Cg are the heat capacities of the components, c and c1 are constants, and the rest has already been explained.)
Given the values of the parameters yielded by the solution of the system of equations, we can easily calculate the extropy function of the model universe. (Hint: calculate the amount of entropy the system would produce by getting to equilibrium at a given instant.) The result is:
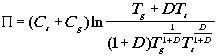 ,
, |
|
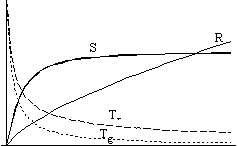
Now let us see some results
of the simulation.
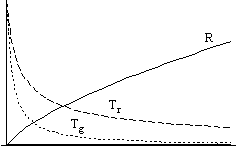
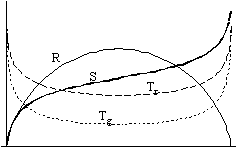
Figure 1. Thermodynamic functions in an open universe
1/a/I. 1/a/II.
 t
t 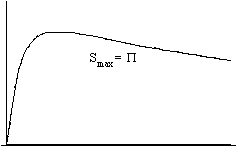 t
t
S = 0
S = 0
1/b/I. 1/b/II.
 t
t  t
t
1/c/I. 1/c/II.
 t
t 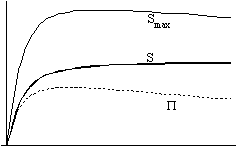 t
t
1/d/I. 1/d/II.
 t
t 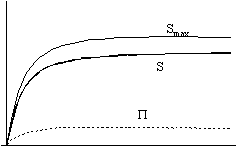 t
t
1/e/I. 1/e/II.
 t
t 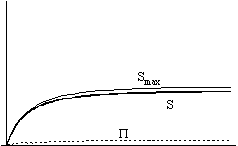 t
t
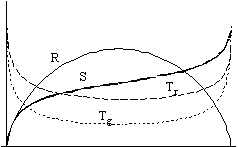
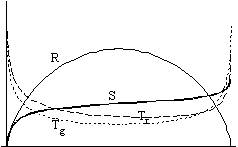
Figure 2. Thermodynamic functions in a closed universe
2/a/I. 2/a/II.
 t
t  t
t
S = 0
S = 0
2/b/I. 2/b/II.
 t
t 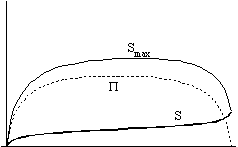 t
t
2/c/I. 2/c/II.
 t
t 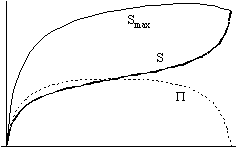 t
t
2/d/I. 2/d/II.
 t
t  t
t
2/e/I. 2/e/II.
 t
t 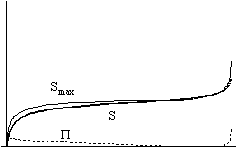 t
t
1.e) Explanation to
the figures
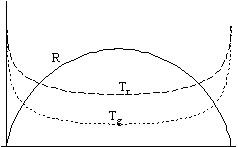
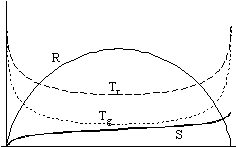
Fig. 1 shows the case of an open universe, while Fig. 2 shows a closed universe. The universe is open when the gravity of the total mass is not enough to stop the expansion: it goes on forever. The universe is closed when the expansion stops at some finite time and the universe starts to contract.
In the left hand figures you can see the graphs of the radius, the temperatures and the entropy, while in the right hand figures you find entropy, extropy and the maximum value of entropy (Smax =P + S).
We increase the strength of the interaction between the components (A) from the top figures towards the bottom ones, the value being 0 in the first line and practically infinitely large in the bottom line.
Let us concentrate on the case of open universe because, according to the recent cosmological views, that seems to be the more realistic case now.
We see that two factors determine the value of entropy:
if the interaction is weak, there is not much
entropy produced;
if the interaction is strong, the temperature
difference is small,
so the interaction process becomes weak again.
Nonetheless, the dependence of extropy on the strength of interaction shows a monotone function: the stronger the interaction is, the smaller the extropy becomes.
Let us now turn to the time-dependence of the parameters.
We can see that no matter how strong the interaction is, the extropy function follows the same qualitative route with time: it increases at the beginning, but later it starts to decrease and it tends to zero as time approaches infinity. It means that there is no way of avoiding the final state of Heat Death - the boring state of absolute, eternal smoothness and peace.
Still, thanks to the expansion of the universe, the temperatures of the two components become different vehemently at the beginning. Therefore, there is an initial increase in the value of extropy, it becomes greater than zero, and the universe leaves its equilibrium state. So the expansion of the universe creates the possibility of all the physical processes of the future: Extropy means process, it means motion and life.
The question today is not the question of the last century:
"Will the universe get to the state of Heat Death,
or can we avoid it?",
but it is the question:
"Why is the universe not in its equilibrium state,
where do the processes come from?"
The notion of extropy can give a plausible answer to both of these
questions.
2. Equilibrium thermodynamics
in economics?
2.a) The difference between two disciplines
For the sake of comprehension, let us turn to an example: why we cannot build the two theories on the same mathematical principles. We take the expressions of energy and of money:
|
|
|
|
|
|
| where
E is energy, p is pressure,
V is volume, Q is heat. |
where
M is money, p is price,
X is (quantity of) product, I is the free flow of money. |
Formally, the two expressions are very similar. BUT there are serious differences under the surface.
Pressure in thermodynamics is a state parameter, while price in economics is not. If we want to have a state parameter in the expression, we take v, which is the value, and write:
In economics, it is postulated that money is a state parameter, so there is no need to declare the conservation law. The parallel between the two disciplines is just formal.
2.b) The similarity
between two disciplines
The difference discussed above might be traced back to the difference
in the conservation laws:
* the total energy in physics is conserved, while
* the total amount of money in economics is not.
Still, in cosmology the conservation law does not seem to hold for
the first sight. Remember Eq. 2: ![]() ,
so the energy is not constant. But it is just the thermodynamic kind of
energy that we have in this expression (internal energy), not the total
energy.
,
so the energy is not constant. But it is just the thermodynamic kind of
energy that we have in this expression (internal energy), not the total
energy.
The total energy is (of course) conserved in cosmology:
Etotal =Egrav +Eint . (13)
In the expansion of the universe, the absolute value of the gravitational energy becomes smaller, therefore the internal energy becomes smaller as well. But it is only the latter kind of energy which thermodynamics deals with.
We see that in the thermodynamic description of cosmology, the internal energy is conserved only locally, and not globally. This local conservation is enough to build a fruitful theory.
In economics, money is conserved locally (that is, generally
there is no source of money, apart from a small number of places). This
analogy suggests the need for a new economic theory.
| REFERENCES
|
| Alpher, R.A. & Marx, Gy.:
The creation of free energy Vistas in Astronomy, Vol. 35 (1992) |
| Kutrovátz, G.:
Termodinamikai folyamatok a kozmológiában [in Hungarian: Thermodynamic processes in cosmology] MA thesis (ELTE university, 1999) |
| Martinás, K.:
Irreversible microeconomics in: Complex systems in natural and economic sciences (eds. K. Martinás and M. Moreau): Proc. of the workshop (Mátrafüred, 1995) |
| Martinás, K.:
Thermodynamics and sustainability: a new approach by extropy Per. Polytech. S. Chem. Eng., Vol. 42 (1998) |
| Marx, Gy.:
Irreverzibilis univerzum [in Hungarian: Irreversible universe] Fizikai Szemle, 38/162 (1988) |